There is a debate in the community about performance metrics and the value of using multi-model ensemble (MME) averages versus single-best or a skill-selected set of models. One perspective may be to view the multi-model ensemble statistics as reflecting the most likely projections, with each individual model simulation representing a plausible future condition of the climate system. In view of this ambiguity and open research problems in this topic, we have pursued various lines of research on this topic.

Highlights:

In one part, we have studied the prediction of climate variables over different time horizons, using Bayesian methodology. We attempt to embed physics-based knowledge and constraints in the data model; for example, the Clausius-Clapeyron (CC) relation is used as part of the data analysis for precipitation and precipitation extremes. There are two approaches to take: we may use the physics-driven relation and use data analytic methods to model the residuals, or we might use the physics-based relation as a constraint for data modeling. As of year 3, much progress has been made on development of a hybrid physics-informed Bayesian scheme for arriving at probability distribution estimates for rainfall extremes. The physics component utilizes the CC; specifically, measures the degree to which rainfall extremes scale per the CC from multiple observational datasets and climate models. In year 4 we addressed the fact that existing studies in Bayesian modelling fail to consider one or more of the following characteristics: multivariate responses, three dimensional spatial indexing set, temporal indexing set, complex dependency structures, the spherical nature of the domains set. Our results using oceanographic variables as our data suggest very complex dependency structures between the temperature, salinity, the ratios of the isotopes of hydrogen and oxygen, and the latitude, longitude, depth of sea, and the time of the year.

In a second study, we compared various techniques to combine multiple GCMs outputs to significantly reduce forecast variability without loss of physical significance. In an application involving land surface temperature, the root mean square error (RMSE) per geographical location for several approaches was evaluated. It was shown that a Multi-task Sparse Structure Learning (MSSL) approach we developed gave significantly better results overall than an average of models, the best model prediction, or ordinary least squares (OLS). MSSL was also better than our Spatially Smooth Multi-Model Regression (S2M2R) model which won the Best Application Paper Award at the 2013 SIAM International Conference on Data Mining. MSSL also seemed to be able to better capture the physical structure of the problem, e.g., Chile and Argentina have quite different climates, even though they are adjacent.

In a third study, we are conducting a broad investigation into a number of topics involving statistical model selection and averaging. For instance, we have investigated thoroughly the model selection approach in a limited linear regression framework, and have completed a considerable part of the study in multiple linear regression frameworks. This study has now also been extended to cases where full statistical model specification may not be available, where there may be infinite dimensional parameters, and potentially high dimensional nuisance parameters. The most general model framework where this methodology might be applicable has been developed, and a branch-off study on model selection in small-area context is under investigation. In this branch study, we are using natural exponential families with quadratic variance function as the model framework, and using empirical predictors of various kinds for a predictive model, and evaluating model ensembles in terms of predictive performances. In more applied work, we also examined the shortcomings of a model for the relationship between minimum pressure and maximum wind speed in a tropical cyclone and improved upon on the model parameter estimates via least squares and maximum likelihood estimation. This study is currently being extended to multivariate objects that are studied simultaneously, and in particular multivariate quantiles. Our aim is to extend the notion of model selection from regression models to a wider class of problems that satisfy some regularity conditions. Another topic in this area is resampling techniques for model selection where only limited data or complex data is available. In year 4, we have now conducted several artificial data driven studies and several alternative methods for statistical model selection, and have shortlisted several promising approaches. In another related development, we have tried to include model selection in the context of functional and semiparametric data. An important component in this arm of the study is to use functional decomposition methods like Fourier transformations or wavelets, establish statistical properties of the coefficients arising from such decomposition, and then use a resampling method to construct other possible paths that the data might have taken. 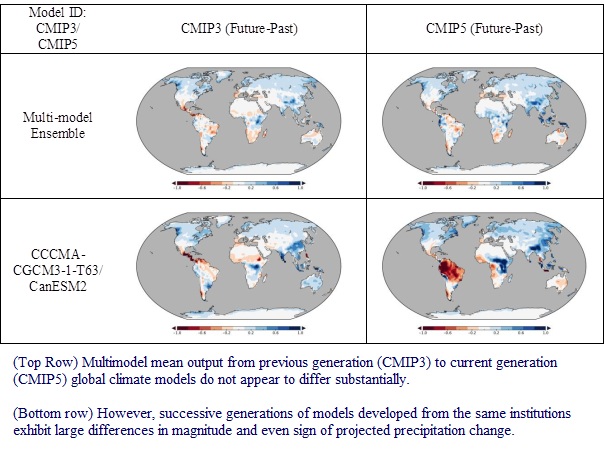In a fourth study, we evaluated the robustness of GCMs in two broad categories: (a) Evaluation of GCMs at regional scales, (b) Assessment of uncertainty in GCM output. Results suggest little change in the central tendency or variability or uncertainty of historical skills or consensus across two generations of models, although there are regions and seasons, at different levels of aggregation, where significant changes, performance improvements, and even degradation in skills, were suggested. The insights may provide directions for further improvements in next generations of climate models, and in the meantime, help inform adaptation and policy. In specific evaluation of US precipitation, our results suggest that while model consensus may be valuable in some regions (e.g., the western United States), overreliance on consensus or multi-model averaging may be dangerous from a policymaking perspective.

People: Banerjee, Chatterjee, Ganguly, Liess, Semazzi, Shekhar